Some variants of the Basel problem
July 4, 2023
This note studies the Basel problem, named after the hometown of Euler. This problem was unsuccessfully attempted by three members of the Bernoulli family before it was famously solved by Euler in 1735. The Euler problem is to explicitly compute $\zeta(2) = \sum_{n=1}^\infty \frac{1}{n^2}$, where $\zeta$ denotes the Riemann zeta function. We know that the sum is convergent by the $p$-series test, but the Basel problem is to compute its explicit value. The result is surprising, so here’s a solution to the Basel problem that I wrote up using complex analytic techniques. Later in this note, I’ll also include my solution to a variant of the Basel problem using Fourier analysis.
The Basel problem
We approach this problem by first studying the complex cotangent function.
Uniform limits of analytic functions
First, we’ll show that the uniform limit of a sequence of holomorphic functions is itself holomorphic on a disk $D$. Suppose $(f_n)_{n \in \mathbb{N}}$ is a sequence of holomorphic functions that uniformly converges to some function $f$ on $D$. Then suppose $T$ is any triangle contained in $D$. Because $f_n$ is holomorphic for all $n \in \mathbb{N}$ we know by Cauchy’s theorem that $\int_{\partial T} f_n(z)\ dz = 0$. Fix $\epsilon > 0$ and choose $N \in \mathbb{N}$ such that $\sup_{z \in D}\ \lvert f(z) - f_n(z) \rvert < \frac{\epsilon}{\operatorname{length}(\partial T)}$ for all $n \geq N$ by uniform convergence. Then, it follows from this that:
\[\begin{align*} \left\lvert \int_{\partial T} f(z)\ dz \right\rvert = \left\lvert \int_{\partial T} (f(z) - f_n(z))\ dz \right\rvert \leq \left( \sup_{z \in \partial T}\ \lvert f(z) - f_n(z) \rvert \right) \cdot \operatorname{length}(\partial T) < \epsilon. \end{align*}\]Hence we deduce that $\int_{\partial T} f(z)\ dz = 0$ for all triangles $T$ contained in $D$, which means that $f$ is holomorphic on $D$ by Morera’s theorem; we have proven our original claim.
The complex cotangent function
We’ll start by defining a function $f$ by the following Laurent series:
\[\begin{align*} f(z) = \frac{1}{z} + \sum_{n=1}^\infty \left( \frac{1}{z-n} + \frac{1}{z+n} \right) = \frac{1}{z} + \sum_{n=1}^\infty \frac{z+n+z-n}{(z-n)(z+n)} = \frac{1}{z} + 2z \sum_{n=1}^\infty \frac{1}{z^2 - n^2}. \end{align*}\]Now it suffices to show that the sum $\sum_{n=1}^\infty \frac{1}{z^2 - n^2}$ converges uniformly on compact subsets $K \subseteq U = \mathbb{C} \setminus \mathbb{Z}$. We know that $S$ is bounded, so suppose $R > 0$ is such that $\lvert z \rvert \leq R$ for all $z \in K$. Also, suppose that $d(K, \mathbb{Z}) = \delta$ for some $\delta > 0$ (since $K$ is compact and $\mathbb{Z}$ is closed in $\mathbb{C}$ and have empty intersection). Then, we know that for $n \leq R$ we have:
\[\begin{align*} \left\lvert \frac{1}{z^2 - n^2} \right\rvert = \left\lvert \frac{1}{z - n} \right\rvert \cdot \left\lvert \frac{1}{z + n} \right\rvert \leq \frac{1}{\delta^2}. \end{align*}\]Similarly, we have for $n > R$ (by the reverse triangle inequality):
\[\begin{align*} \left\lvert \frac{1}{z^2 - n^2} \right\rvert \leq \left\lvert \frac{1}{\lvert z \rvert^2 - n^2} \right\rvert = \frac{1}{n^2 - \lvert z \rvert^2} \leq \frac{1}{n^2 - R^2}. \end{align*}\]Then, we know that $\sup_{z \in K}\ \left\lvert \frac{1}{z^2 - n^2} \right\rvert \leq \frac{1}{\delta^2}$ for $n \leq R$ and $\sup_{z \in K}\ \left\lvert \frac{1}{z^2 - n^2} \right\rvert \leq \frac{1}{n^2 - R^2}$ for $n > R$. Now, we will show that the following sum is convergent:
\[\begin{align*} \sum_{n \leq R} \left( \frac{1}{\delta^2} \right) + \sum_{n > R} \left( \frac{1}{n^2 - R^2} \right). \end{align*}\]Then, notice that $\sum_{n > R} \left( \frac{1}{n^2 - R^2} \right)$ is convergent by limit comparison to $\sum_{n > R} \frac{1}{n^2}$ (which converges by the $p$-series test); namely, we have:
\[\begin{align*} \lim_{n \to \infty} \left( \frac{n^2}{n^2 - R^2} \right) = \lim_{n \to \infty} \left( \frac{1}{1 - \frac{R^2}{n^2}} \right) = 1. \end{align*}\]Since this limit is finite, we deduce that $\sum_{n > R} \left( \frac{1}{n^2 - R^2} \right)$ is convergent. Furthermore, $\sum_{n \leq R} \left( \frac{1}{\delta^2} \right)$ is clearly convergent as it is a finite sum of constant terms. Thus we deduce that the above sum is indeed convergent as desired, which means that $\sum_{n=1}^\infty \frac{1}{z^2 - n^2}$ converges uniformly on $K$ (and in fact converges absolutely) by the dominated convergence theorem.
Notice that if we define $f_N(z) = \frac{1}{z} + \sum_{n=1}^N \left( \frac{1}{z-n} + \frac{1}{z+n} \right)$ then $f_N$ is holomorphic because it is the finite sum of rational functions with nonzero denominator. Then, since $f_N \to f$ converges uniformly, $f$ must also be holomorphic by our first result.
Because the series defining $f$ converges absolutely and uniformly, we can rewrite $f$ in the following form:
\[\begin{align*} f(z) = \frac{1}{z} + \sum_{n=1}^\infty \left( \frac{1}{z - n} + \frac{1}{z + n} \right) = \sum_{n \in \mathbb{Z}} \frac{1}{z - n}. \end{align*}\]We compute as follows, since the series defining $f$ converges absolutely and we can rearrange the series (making the assignment $n^\prime = n - 1$):
\[\begin{align*} f(z + 1) = \sum_{n \in \mathbb{Z}} \frac{1}{z + 1 - n} = \sum_{n^\prime \in \mathbb{Z}} \frac{1}{z - n^\prime} = f(z). \end{align*}\]Also, we see that (making the assignment $n^\prime = -n$):
\[\begin{align*} f(-z) = \sum_{n \in \mathbb{Z}} \frac{1}{-z - n} = \sum_{n^\prime \in \mathbb{Z}} \frac{1}{-z + n^\prime} = -\sum_{n^\prime \in \mathbb{Z}} \frac{1}{z - n^\prime} = -f(z). \end{align*}\]Hence $f$ is odd with period 1. Next, suppose $z = a + bi$ be such that $\lvert \Im(z) \rvert = b > 1000$; in particular, we want $z$ to stay bounded away from the real axis. Because $f$ is periodic, we may assume that $0 \leq \Re(z) = a < 1$. We’ll now show that $f$ is bounded away from the real axis. Notice that we now have:
\[\begin{align*} \left\lvert \sum_{n=1}^\infty \left( \frac{1}{z - n} + \frac{1}{z + n} \right) \right\rvert & = \left\lvert \sum_{n=1}^\infty \frac{1}{a + bi - n} + \frac{1}{a + bi + n} \right\rvert \\ & \leq \left\lvert \sum_{n=1}^{\lceil \lvert b \rvert \rceil} \left( \frac{1}{a + bi - n} + \frac{1}{a + bi + n} \right) \right\rvert + \left\lvert \sum_{n = \lceil \lvert b \rvert \rceil + 1}^\infty \left( \frac{1}{a + bi - n} + \frac{1}{a + bi + n} \right) \right\rvert. \end{align*}\]Then, notice that, since $d(bi, \mathbb{R}) = b$ we have $\lvert a + bi - n \rvert \geq \lvert bi \rvert > 1000$ and $\lvert a + bi + n \rvert \geq \lvert bi \rvert > 1000$. Hence, we have the following bound on the first sum by the triangle inequality:
\[\begin{align*} \left\lvert \sum_{n=1}^{\lfloor \lvert b \rvert \rfloor} \left( \frac{1}{a + bi - n} + \frac{1}{a + bi + n} \right) \right\rvert & \leq \sum_{n=1}^{\lceil \lvert b \rvert \rceil} \left( \left\lvert \frac{1}{a + bi - n} \right\rvert + \left\lvert \frac{1}{a + bi + n} \right\rvert \right) \\ & \leq \sum_{n=1}^{\lceil \lvert b \rvert \rceil} \left( \frac{1}{1000} + \frac{1}{1000} \right) \\ & \leq \sum_{n=1}^{2000} \frac{1}{500} \\ & = 4. \end{align*}\]Now we bound the right hand sum. We know that $\lvert b \rvert \leq \lvert a + bi \rvert \leq 1 + \lvert b \rvert$ by the triangle inequality and since $d(bi, \mathbb{R}) = \lvert b \rvert$. Similarly we find by the triangle inequality that $\lvert a + bi + n \rvert \geq \lvert n \rvert = n$. Thus we have (since $0 \leq a < 1$):
\[\begin{align*} \lvert z^2 - n^2 \rvert = \lvert a^2 + 2abi - b^2 - n^2 \rvert \geq \lvert a^2 - b^2 - n^2 \rvert \geq b^2 + n^2 - 1. \end{align*}\]Therefore, we obtain by the triangle inequality:
\[\begin{align*} \left\lvert \sum_{n = \lceil \lvert b \rvert \rceil + 1}^\infty \left( \frac{1}{z - n} + \frac{1}{z + n} \right) \right\rvert & = \left\lvert \frac{1}{z} + 2z \sum_{n = \lceil \lvert b \rvert \rceil + 1}^\infty \frac{1}{z^2 - n^2} \right\rvert \\ & \leq \frac{1}{\lvert z \rvert} + 2 \lvert z \rvert \sum_{n = \lceil \lvert b \rvert \rceil + 1}^\infty \frac{1}{\lvert z^2 - n^2 \rvert} \\ & \leq \frac{1}{\lvert b \rvert} + 2 \sum_{n = \lceil \lvert b \rvert \rceil + 1}^\infty \frac{\lvert b \rvert + 1}{b^2 + n^2 - 1}. \end{align*}\]Then, notice that $\frac{1}{\lvert b \rvert}$ is a decreasing function in $\lvert b \rvert$. Similarly, notice that $\frac{\lvert b \rvert + 1}{b^2 + n^2 - 1}$ is a decreasing function in $\lvert b \rvert$ when $n > \lvert b \rvert$ (we can find this by taking the partial derivative). Therefore, since $\lvert b \rvert > 1000$ by hypothesis, we get the following inequality:
\[\begin{align*} \frac{1}{\lvert b \rvert} + 2 \sum_{n = \lceil \lvert b \rvert \rceil + 1}^\infty \frac{\lvert b \rvert + 1}{b^2 + n^2 - 1} \leq \frac{1}{1000} + 2002 \sum_{n=1001}^\infty \frac{1}{1000^2 + n^2 - 1}. \end{align*}\]We can now bound $\sum_{n=5}^\infty \frac{1}{n^2}$ as follows:
\[\begin{align*} \sum_{n=5}^\infty \frac{1}{n^2} \leq \sum_{n=5}^\infty \frac{1}{n^2-1} = \frac{1}{2} \sum_{n=5}^\infty \left( \frac{1}{n-1} - \frac{1}{n+1} \right). \end{align*}\]This sum telescopes and the above inequality implies that $\sum_{n=5}^\infty \frac{1}{n^2} \leq \frac{1}{2} \cdot \left( \frac{1}{4} + \frac{1}{5} \right) \leq \frac{1}{4}$. Now, we know that, since $n > b \geq 1000$:
\[\begin{align*} \sum_{n=1001}^\infty \frac{1}{1000^2 + n^2 - 1} \leq \sum_{n=1001}^\infty \frac{1}{n^2} \leq \sum_{n=5}^\infty \frac{1}{n^2} \leq \frac{1}{4}. \end{align*}\]Hence, substituting in the above, we find that:
\[\begin{align*} \left\lvert \sum_{n = \lceil \lvert b \rvert \rceil + 1}^\infty \left( \frac{1}{z - n} + \frac{1}{z + n} \right) \right\rvert \leq \frac{1}{1000} + 2002 \sum_{n=1001}^\infty \frac{1}{1000^2 + n^2 - 1} \leq 1 + 2000 \cdot \frac{1}{4} = 501. \end{align*}\]Thus we deduce from our original inequality that:
\[\begin{align*} \left\lvert \sum_{n=1}^\infty \left( \frac{1}{z - n} + \frac{1}{z + n} \right) \right\rvert \leq 4 + 501 = 505 < 1000. \end{align*}\]We’ll now show that $f$ and $\pi \cot(\pi z)$ have the same poles and hence their difference will be holomorphic. First, we know that $f$ is periodic so we’ll just consider the pole at $z = 0$. Let $\gamma$ be the positively-oriented circle of radius $\frac{1}{2}$ centered at $z = 0$. Now, recall that we can interchange the sum in $f$ with an integral because the sum converges uniformly and absolutely. Notice also that $f$ has a pole of order one at zero and (since we showed that the below sum converges absolutely) integrating $f$ around $\gamma$ yields:
\[\begin{align*} \int_\gamma f(z)\ dz = \int_\gamma \left( \sum_{n \in \mathbb{Z}} \frac{1}{z - n} \right)\ dz = \sum_{n \in \mathbb{Z}} \int_\gamma \frac{1}{z - n}\ dz = \int_\gamma \frac{1}{z}\ dz = 2\pi i. \end{align*}\]Now, we want to find $a_{-1}$ in the series expansion of $\pi \cot(\pi z)$ so we compute:
\[\begin{align*} a_{-1} = 2\pi i \lim_{z \to 0}\ \pi z \cot(\pi z) = 2 \pi^2 i \lim_{z \to 0} \frac{z \cos(\pi z)}{\sin(\pi z)}. \end{align*}\]Using l’Hôpital’s rule, this limit can be rewritten as:
\[\begin{align*} 2 \pi^2 i \lim_{z \to 0} \frac{\cos(\pi z) - \pi z \sin(\pi z)}{\pi \cos(\pi z)} = 2 \pi^2 i \lim_{z \to 0} \frac{\cos(\pi z)}{\pi \cos(\pi z)} = 2\pi i. \end{align*}\]Then, this means that $\pi \cot(\pi z)$ has a series expansion of the following form:
\[\begin{align*} \pi \cot(\pi z) = 2\pi i z^{-1} + \sum_{k=0}^\infty a_k z^k. \end{align*}\]Similarly, $f$ has a series expansion of the following form:
\[\begin{align*} f(z) = 2\pi i z^{-1} + \sum_{k=0}^\infty b_k z^k. \end{align*}\]Hence we deduce that $g(z) = \pi \cot(\pi z) - f(z)$ has the following form:
\[\begin{align*} g(z) = \pi \cot(\pi z) - f(z) = \sum_{k=0}^\infty (a_k - b_k) z^k. \end{align*}\]Since $g(z)$ has a power series representation, we deduce that $g$ is entire. Furthermore, we can show that $g(z) = \pi \cot(\pi z) - f(z)$ is bounded. Notice that $\pi \cot(\pi z)$ is bounded away from the real axis; namely, we have:
\[\begin{align*} \pi \cot(\pi z) = \pi i \left( \frac{e^{i \pi z} + e^{-i \pi z}}{e^{i \pi z} - e^{-i \pi z}} \right) = \pi i \left( \frac{e^{2\pi i z} + 1}{e^{2\pi i z} - 1} \right) = \pi i \left( 1 + \frac{2}{e^{2\pi i z} - 1} \right) \end{align*}\]Let $z = a + bi$ and assume without loss of generality $\Re(z) \leq 1$ since $\pi \cot(\pi z)$ is periodic with period 1. Now, we have by the reverse triangle inequality:
\[\begin{align*} \left\lvert \pi i \left( \frac{e^{i \pi z} + e^{-i \pi z}}{e^{i \pi z} - e^{-i \pi z}} \right) \right\rvert & = \left\lvert \pi i \left( 1 + \frac{2}{e^{2\pi i z} - 1} \right) \right\rvert \\ & \leq \left( \lvert \pi i \rvert + \left\lvert \frac{2}{e^{2\pi i z} - 1} \right\rvert \right) \\ & \leq \pi + \left\lvert \frac{2 \pi}{e^{2\pi i z} - 1} \right\rvert \\ & \leq \pi + 2 \pi \frac{1}{\lvert \lvert e^{2\pi i z} \rvert - 1 \rvert} \\ & = \pi + 2 \pi \frac{1}{\lvert e^{-2\pi b} - 1 \rvert}. \end{align*}\]Then, it becomes clear by limit properties that we have the limits $\lim_{b \to \infty}\ \left( \pi + 2 \pi \frac{1}{\lvert e^{-2\pi b} - 1 \rvert} \right) = 3 \pi$ and $\lim_{b \to -\infty}\ \left( \pi + 2 \pi \frac{1}{\lvert e^{-2\pi b} - 1 \rvert} \right) = \pi$. Therefore we deduce that we can choose $R > 0$ such that $\lvert \pi \cot(\pi z) \rvert \leq 3\pi$ when $\Im(z) > R$. Then, we know that $g(z) = \pi \cot(\pi z) - f(z)$ is bounded by the reverse triangle inequality when $\Im(z) > R$ for some $R > 0$. Furthermore, this function is holomorphic on the compact set ${ z \in \mathbb{C} : \Re(z) \leq 1, \Im(z) \leq R }$ and therefore bounded on this set. Since this function is periodic with period 1 (it is the difference of functions with period 1) we deduce that $g$ is bounded on $\mathbb{C}$. \par Now, since $g$ is entire and bounded, we deduce that $g$ is constant by Liouville’s theorem. However, since $f(z)$ and $\pi \cot(\pi z)$ are both clearly odd functions, so too is $g$. This means that $g$ is identically zero, and we conclude that:
\[\begin{align*} f(z) = \frac{1}{z} + \sum_{n=1}^\infty \left( \frac{1}{z-n} + \frac{1}{z+n} \right) = \pi \cot(\pi z). \end{align*}\]Now that we have a handle on $f$, we need to prove one more lemma before arriving at the main result.
Convergence on compact subsets
Suppose $f_n, f$ are holomorphic and $f_n \to f$ converges uniformly on compact subsets of $\Omega$. Then, we’ll show that $f_n^\prime \to f^\prime$ on compact subsets of $\Omega$ as well. Let $K \subseteq \Omega$ be a compact set. Notice that $\Omega$ is clearly open so we can choose $\delta_x > 0$ for each $x \in K$ such that $\overline{B_{\delta_x}(x)} \subseteq \Omega$. Then, it’s clear that ${ B_{\delta_x}(x) }_{x \in K}$ forms an open cover for $K$ and by compactness we can choose a finite subcover (after renaming) called ${ B_{\delta_k}(x_k) }_{k=1}^r$. Fix $\epsilon > 0$ and choose $N \in \mathbb{N}$ such that for all $n \geq N$ we have $\sup_{z \in K}\ \lvert f(z) - f_n(z) \rvert < \epsilon$ by uniform convergence of $(f_n)$ to $f$ on compact subsets of $\Omega$. Now, for all $1 \leq k \leq r$ we know by the Cauchy inequalities that:
\[\begin{align*} \lvert f^\prime(z) - f_N^\prime(z) \rvert \leq \frac{\sup_{z \in B_{\delta_k}(x_k)}\ \lvert f(z) - f_N(z) \rvert}{\delta_k^2} < \frac{\epsilon}{\delta_k^2}. \end{align*}\]Since $\epsilon$ could have been chosen arbitrarily small, we deduce that $(f_n^\prime)$ converges uniformly to $f^\prime$ on $B_{\delta_k}(x_k)$ for all $1 \leq k \leq r$. Now, for any $\epsilon > 0$ there exist indices $N_1, N_2, \cdots, N_r$ such that $n \geq N_k$ implies that $\sup_{z \in B_{\delta_k}(x_k)}\ \lvert f^\prime(z) - f_n^\prime(z) \rvert < \epsilon$. Finally, we can choose $N = \max_k { N_k }$ so that $n \geq N$ implies that $\sup_{z \in K}\ \lvert f^\prime(z) - f_n^\prime(z) \rvert < \epsilon$. Hence we have shown that $f_n^\prime$ converges uniformly to $f^\prime$ on compact subsets of $\Omega$. Armed with this lemma and our previous results about $f$, we can begin to see why all of this relates to the Basel problem.
Solving the Basel problem
We’ll now differentiate both sides of the identity that we derived for $f$. First, we find:
\[\begin{align*} (\pi \cot(\pi z))^\prime = \pi i \left( \frac{e^{i \pi z} + e^{-i \pi z}}{e^{i \pi z} - e^{-i \pi z}} \right)^\prime = \frac{4 \pi^2}{(e^{i \pi z} - e^{-i \pi z})^2} = -\frac{\pi^2}{\sin^2(\pi z)}. \end{align*}\]Now, notice that we can differentiate under the sum because the given sum converges uniformly on compact sets (as shown previously) and we can always choose a compact set in $U = \mathbb{C} \setminus \mathbb{Z}$ containing any point $x \in U$ because $U$ is clearly open. Hence, we find:
\[\begin{align*} \left( \sum_{n \in \mathbb{Z}} \frac{1}{z - n} \right)^\prime = \sum_{n \in \mathbb{Z}} \left( \frac{1}{z - n} \right)^\prime = \sum_{n \in \mathbb{Z}} -\frac{1}{(z - n)^2} = -\sum_{n \in \mathbb{Z}} \frac{1}{(z - n)^2}. \end{align*}\]Hence, we can use our identity for $f$ to conclude that:
\[\begin{align*} -\sum_{n \in \mathbb{Z}} \frac{1}{(z - n)^2} = -\frac{\pi^2}{\sin^2(\pi z)} \implies \sum_{n \in \mathbb{Z}} \frac{1}{(z - n)^2} = \frac{\pi^2}{\sin^2(\pi z)}. \end{align*}\]Note that the sum of the even terms in the series defining $\zeta(2)$ is given by:
\[\begin{align*} \sum_{n=1}^\infty \frac{1}{(2n)^2} = \sum_{n=1}^\infty \frac{1}{4n^2} = \frac{1}{4} \sum_{n=1}^\infty \frac{1}{n^2} = \frac{1}{4} \zeta(2). \end{align*}\]Since the sum $\zeta(2)$ is equal to the sum of the even terms and odd terms, we deduce that the sum of the odd terms must be given by:
\[\begin{align*} \sum_{n=1}^\infty \frac{1}{(2n - 1)^2} = \frac{3}{4} \zeta(2). \end{align*}\]Using this result, we obtain:
\[\begin{align*} \frac{3}{4} \zeta(2) = \sum_{n=1}^\infty \frac{1}{(2n - 1)^2} = \frac{1}{4} \sum_{n=1}^\infty \frac{1}{\left( \frac{1}{2} - n \right)^2} \implies \zeta(2) = \frac{1}{3} \sum_{n=1}^\infty \frac{1}{\left( \frac{1}{2} - n \right)^2}. \end{align*}\]Now we compute that (since the following sums are absolutely convergent by limit comparison to $\sum \frac{1}{n^2}$):
\[\begin{align*} \sum_{n \in \mathbb{Z}} \frac{1}{\left( \frac{1}{2} - n \right)^2} = \sum_{n=-\infty}^{-1} \frac{1}{\left( \frac{1}{2} - n \right)^2} + 4 + \sum_{n=1}^\infty \frac{1}{\left( \frac{1}{2} - n \right)^2}. \end{align*}\]However, notice that we have the following for all $R > 0$:
\[\begin{align*} \sum_{n=-R}^{-1} \frac{1}{\left( \frac{1}{2} - n \right)^2} = \sum_{n=2}^R \frac{1}{\left( \frac{1}{2} - n \right)^2} = -4 + \sum_{n=1}^R \frac{1}{\left( \frac{1}{2} - n \right)^2}. \end{align*}\]Therefore, taking the limit as $R \to \infty$ we have:
\[\begin{align*} \sum_{n \in \mathbb{Z}} \frac{1}{\left( \frac{1}{2} - n \right)^2} = \left( -4 + \sum_{n=1}^\infty \frac{1}{\left( \frac{1}{2} - n \right)^2} \right) + 4 + \sum_{n=1}^\infty \frac{1}{\left( \frac{1}{2} - n \right)^2} = 2 \sum_{n=1}^\infty \frac{1}{\left( \frac{1}{2} - n \right)^2} \implies \zeta(2) = \frac{1}{6} \sum_{n \in \mathbb{Z}} \frac{1}{\left( \frac{1}{2} - n \right)^2}. \end{align*}\]Finally, recall that (by our previous result) we have:
\[\begin{align*} \sum_{n \in \mathbb{Z}} \frac{1}{\left( \frac{1}{2} - n \right)^2} = \frac{\pi^2}{\sin^2\left( \frac{\pi}{2} \right)} = \pi^2. \end{align*}\]Thus we deduce that $\zeta(2) = \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}$, which is a well-known but beautiful and surprising result!
A variant of the Basel problem
One variant of the Basel problem is to compute $\sum_{n=1}^\infty \frac{1}{n^2 + 1}$ and the associated alternating series $\sum_{n=1}^\infty \frac{(-1)^n}{n^2 + 1}$. This problem turns out to be much easier and we can compute the sums using Fourier series. First, we’ll compute the Fourier series for $f(x) = e^x$ on $[-\pi, \pi]$:
\[\begin{align*} a_0 = \frac{1}{\pi} \int_{-\pi}^\pi e^x\ dx = \frac{e^\pi - e^{-\pi}}{\pi} = \frac{2\sinh(\pi)}{\pi}. \end{align*}\]We then compute the coefficients $a_n$ on the cosine terms using integration by parts:
\[\begin{align*} a_n = \frac{1}{\pi} \int_{-\pi}^\pi e^x \cos(nx)\ dx = \frac{2 \sinh(\pi) \cos(n\pi)}{\pi(n^2 + 1)}. \end{align*}\]Similarly, we see that the coefficients on the sine terms are given by:
\[\begin{align*} b_n = \frac{1}{\pi} \int_{-\pi}^\pi e^x \sin(nx)\ dx = \frac{-2n \sinh(\pi) \cos(n\pi)}{\pi(n^2 + 1)}. \end{align*}\]Then, we write the Fourier series for $f(x)$ as follows:
\[\begin{align*} f(x) = e^x = \frac{\sinh(\pi)}{\pi} + \sum_{n=1}^\infty \frac{2 \sinh(\pi) \cos(n\pi)}{\pi(n^2 + 1)} \cos(nx) + \sum_{n=1}^\infty \frac{-2n \sinh(\pi) \cos(n\pi)}{\pi(n^2 + 1)} \sin(nx). \end{align*}\]To check our work, here’s a drawing of this Fourier series up to the first 20 terms:
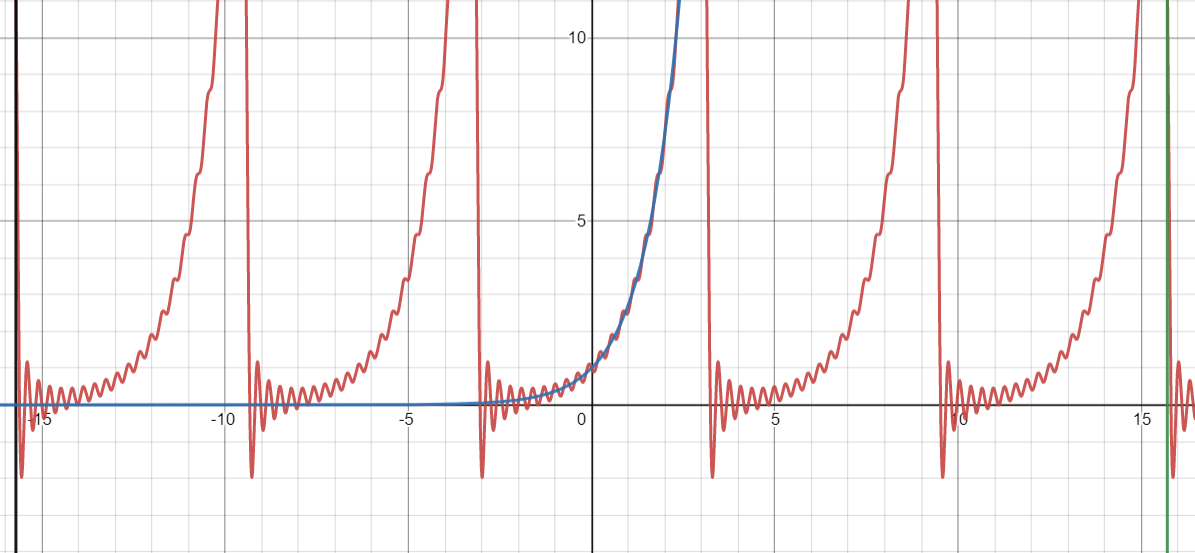
A drawing of the Fourier series for $e^x$ using a partial sum up to 20 terms.
If we set $x = 0$ in the above Fourier series for $e^x$, we can compute the alternating series:
\[\begin{align*} e^0 = 1 & = \frac{\sinh(\pi)}{\pi} + \sum_{n=1}^\infty \frac{2 \sinh(\pi) \cos(n\pi)}{\pi(n^2 + 1)} \cos(0) + \sum_{n=1}^\infty \frac{-2n \sinh(\pi) \cos(n\pi)}{\pi(n^2 + 1)} \sin(0) \\ & = \frac{\sinh(\pi)}{\pi} + \sum_{n=1}^\infty \frac{2 \sinh(\pi) (-1)^n}{\pi(n^2 + 1)} \implies \frac{\pi - \sinh(\pi)}{2 \sinh(\pi)} = \sum_{n=1}^\infty \frac{(-1)^n}{n^2 + 1} \\ & \implies \sum_{n=1}^\infty \frac{(-1)^n}{n^2 + 1} = \frac{1}{2} \left( \frac{\pi}{\sinh(\pi)} - 1 \right). \end{align*}\]On the other hand, if we use the above Fourier series to construct a series for $\cosh(\pi)$, we find:
\[\begin{align*} \cosh(\pi) = \frac{e^{-\pi} + e^\pi}{2} & = \frac{\sinh(\pi)}{\pi} + \sum_{n=1}^\infty \frac{2 \sinh(\pi) \cos(n\pi)}{\pi(n^2 + 1)} \cos(n\pi) + \sum_{n=1}^\infty \frac{-2n \sinh(\pi) \cos(n\pi)}{\pi(n^2 + 1)} \sin(-n\pi) \\ & = \frac{\sinh(\pi)}{\pi} + \sum_{n=1}^\infty \frac{2 \sinh(\pi)}{\pi(n^2 + 1)} \implies \frac{\pi \cosh(\pi) - \sinh(\pi)}{2\sinh(\pi)} = \sum_{n=1}^\infty \frac{1}{n^2 + 1} \\ & \implies \sum_{n=1}^\infty \frac{1}{n^2 + 1} = \frac{1}{2} \left( \frac{\pi}{\tanh(\pi)} - \frac{1}{2} \right). \end{align*}\]This is a neat result, and many similar sums can be explicitly computed using Fourier series as shown here.